Now the electronic system is self-consistent it is possible to evaluate the forces on the atoms in order to optimise the structure.
The forces are determined from the gradient of the free energy, F determined above, with respect to displacement,
| (42) |
These forces can be determined analytically by considering the change
in each term in the total energy for a displacement of ![]() . Thus
. Thus
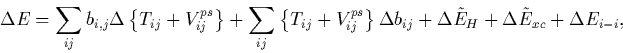
where
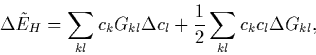

These are rearranged and substitutions made to eliminate ![]() and
and ![]() , leaving terms in only
, leaving terms in only ![]() and
and ![]() .
. ![]() contains terms in
contains terms in ![]() and
and ![]() which can be determined from
Equations 3.2.23 and 3.2.27. Although Tij and Sij
only depend on Rla through the basis functions,
which can be determined from
Equations 3.2.23 and 3.2.27. Although Tij and Sij
only depend on Rla through the basis functions, ![]() , the pseudopotential term is also dependent on Rla
due to
, the pseudopotential term is also dependent on Rla
due to ![]() ; this is determined by
integrating by parts to replace with terms in
; this is determined by
integrating by parts to replace with terms in ![]() :
:
The forces are relatively quick to evaluate compared to determination of the self-consistent energy.