The Hartree Equations

The Hartree equations were derived by considering the electronic wavefunction as a product of many single particle wavefunctions, $\psi_\lambda$, each subject to its own external potential. Thus

The Schrödinger equation for each single particle state, $\lambda$,is given by

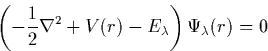$$\left(- \frac{1}{2}\nabla^2 + V(r) - E_\lambda \right) \Psi_\lambda(r) = 0$$ (3)

Hartree suggested that in a many electron system it was possible to replace V(r) with V_eff(r), which included the mean electrostatic potential from all of the electrons [13]. This leads to the Hartree self-consistent equations

The total many body wavefunction is then formed as the product of these one-electron spin-orbitals. V(r) is the potential due to the ions. This simple approximation leads to surprisingly accurate results, but suffers from the lack of electronic exchange, i.e. the many body wavefunction, $\Psi(r,R)$ is not antisymmetric with respect to a switching of two of the electrons. This is in breach of the Pauli principle, which in general imposes a change of sign of the total wavefunction when two electrons are switched, and in the independent electron approximation described above, does not allow more than one electron to occupy a given state.