Self-consistency

Self-consistency involves redistribution of charge throughout the cluster until a minimum energy is reached, thereby hopefully producing an accurate simulation of the charge distribution in an equivalent real system. This equilibrium distribution of charge for a given set of atomic coordinates is achieved by iteratively solving the Kohn-Sham equations until the charge density distribution produced by the Kohn-Sham orbitals gives the same potential that was used to generate it.

In order to achieve this, a first guess set of charge density coefficients, c_k and d_k,s are required; initially we take these from the neutral atom cases but during structural optimisation they are taken from the result of the previous iteration. The Kohn-Sham equations are then solved to determine the density matrix, b_ij,s, which is then used to produce a set of output charge density coefficients, c_k⁰, d_k,s⁰ (Equations 3.2.10 and 3.2.19).

The next choice of charge density coefficients are formed from a weighted combination of the previous two, i.e.

c'_k = c_k + w (c⁰_k - c_k).

The choice of weighting factor, w, is important. If we solve once for a particular value of w (`w₁') giving a specific charge density c⁰_1k, then the deviation from self-consistency of c_k is given by

$$e_k = \frac{(1 - w)(c_k - c_k^0)}{w} - \frac{(c^0_{1k} - c_k)}{w_1}.$$ (39)

This e_k can be used to form a pseudo-charge density, $\sum_k e_k g_k({\bf r})$ which has a corresponding electrostatic energy,

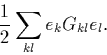$$\frac{1}{2} \sum_{kl} e_k G_{kl} e_l.$$ (40)

w is then chosen by minimising this energy. In practise this can be generalised to include the coefficients from all of the previous iterations, and the cycle converges exponentially, normally in only a few iterations (six or so).