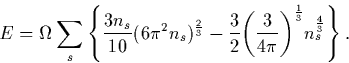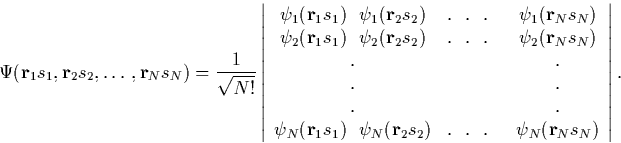
The lack of exchange in Hartree theory is overcome using Hartree-Fock theory, where the many body electronic wavefunction is rewritten [14]. Instead of using a simple product wavefunction, (Equation 2.1.5 above), a Slater determinant is used,
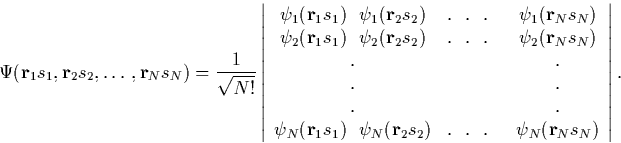
Incorporating electron spin through a spin function, ![]() ,this can be rewritten as
,this can be rewritten as
![]()
![]()
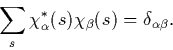
We can define the electron density in terms of these orbitals,
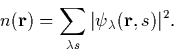
In order to find the ground state it is necessary to minimise the
energy while keeping the orbitals, ![]() , orthonormal. This
is done by applying the variational principle, adding Lagrange
multipliers,
, orthonormal. This
is done by applying the variational principle, adding Lagrange
multipliers, ![]() to Equation 2.1.7,
to Equation 2.1.7,
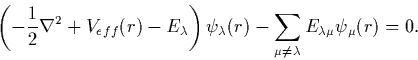
These set of equations are known as the Hartree-Fock equations.
Writing them more completely, for a given orbital, ![]() ,
,
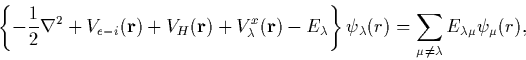 |
(4) |
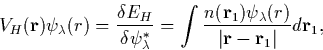

with the orthonormality constraint
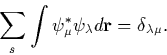
Diagonalising ![]() removes the Lagrange multiplier term on
the right hand side, and the equation can then be solved
self-consistently. To find the total energy, ETOT,
Equation 2.2.10 is multiplied by
removes the Lagrange multiplier term on
the right hand side, and the equation can then be solved
self-consistently. To find the total energy, ETOT,
Equation 2.2.10 is multiplied by ![]() ,integrated over r and summed over s and
,integrated over r and summed over s and ![]() to give
to give
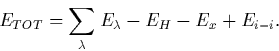
![]() is the ionisation energy for the
is the ionisation energy for the ![]() electron
excluding any redistribution in the remaining orbitals once an
electron is removed.
electron
excluding any redistribution in the remaining orbitals once an
electron is removed.
The orbitals are normally expanded in terms of plane waves, and for a homogeneous electron gas the exact plane wave solution is given by
![]()
In the spin polarised case these are split into the spin `up' and spin `down' populations, each with its own Fermi wavevector; the total energy is a sum of these two populations (ns is the electron density of spin state s). For the homogeneous electron gas this is given by