Parameterising the correlation energy

The correlation energy, E_c, for a homogeneous electron gas comes from a set of quantum Monte Carlo calculations performed by Ceperley and Alder [20]. These were later parameterised by Perdew and Zunger [21]. Slight improvements to these parameterisations have been made since, for example Perdew and Wang [22], but AIMPRO uses the Perdew and Zunger parameterisations in order to remain consistent with the pseudopotential parameters of Bachelet, Hamman and Schlüter [23] (see Section 2.7 below).

The results of Ceperley and Alder apply to low density electron gases, and can be combined with results from perturbation theory for high density gases to cover a wide density range. Defining the correlation energy per electron, $\varepsilon_c$, polarisation $\xi$ and Wigner-Seitz radius of each electron, r_s as:

$$E_c = \Omega n\varepsilon_c(n,\xi), ~~~ \xi = \frac{(n_\upa... ...arrow)}{n},~~~ r_s={\left(\frac{4\pi n}{3}\right)}^\frac{1}{3},$$

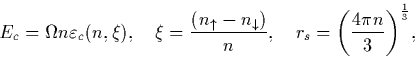
where n is the electron density, for the non-polarised ($\xi=0$) and fully-polarised ($\xi=1$) cases, $\varepsilon_c$ is given by[21]:

 

$$\varepsilon_c = \begin{cases} \gamma \left\{ 1 + \beta_1 \s... ... &r_s \geq 1\\ B + (A + Cr_s)\ln(r_s) + Dr_s&r_s < 1\end{cases}$$ (8)

 

$$\gamma \beta_1 \beta_2$$

Non-polarised -0.1423 1.0529 0.3334

Polarised -0.0843 1.3981 0.2611

A B C D

Non-polarised 0.0311 -0.0480 0.0020 -0.0116

Polarised 0.0155 -0.0269 0.0007 -0.0048

The value of the coefficients $\gamma$, $\beta_1$ and $\beta_2$ are given in Table 2.1. When the gas is only partially polarised ($0 < \xi < 1$), an average of the polarised and non-polarised cases is taken[24],

It is possible to simplify these expressions however; to a good approximation the non-polarised and fully polarised energies vary as $\alpha n^{s_1}$ and $\beta n^{s_2}$ respectively. Therefore for the exchange-correlation energy used in AIMPRO, we use a simplified expression:

 

i A_i p_i q_i

1 -0.9305 0.3333 0.0000

2 -0.0361 0.0000 0.0000

3 0.2327 0.4830 1.0000

4 -0.2324 0.0000 1.0000

i A'_i p'_i q'_i

1 -0.9305 0.3333 0.0000

2 -0.0375 0.1286 0.0000

3 -0.0796 0.0000 0.1286

The coefficients, A_i, p_i and q_i are given in Table 2.2. For larger density values (n > 1), an alternative set of parameters are used, A'_i, p'_i and q'_i (also listed in Table 2.2), which are more accurate in the high density regime. The error when using these approximations is normally less than 3% for densities up to n = 15. For calculations such as these with no heavier metal impurities, the density is normally in the range 0 < n < 1.