Evaluation of Forces

Now the electronic system is self-consistent it is possible to evaluate the forces on the atoms in order to optimise the structure.

The forces are determined from the gradient of the free energy, F determined above, with respect to displacement,

$$f_{la} = -\frac{\partial F}{\partial R_{la}}$$ (42)

These forces can be determined analytically by considering the change in each term in the total energy for a displacement of $\Delta R_{la}$. Thus

$$\Delta E = \sum_{ij} b_{i,j} \Delta \left\{ T_{ij} + V_{ij}^... ... + \Delta \tilde{E}_H + \Delta \tilde{E}_{xc} + \Delta E_{i-i},$$

where

$$\Delta \tilde{E}_H = \sum_{kl}c_kG_{kl}\Delta c_l + \frac{1}{2} \sum_{kl} c_k c_l \Delta G_{kl},$$

$$\Delta \tilde{E}_{xc} = \sum_{k,s} \varepsilon_{k,s}\Delta d_{k,s} + \sum_{k,s} d_{k,s}\Delta \varepsilon_{k,s}.$$

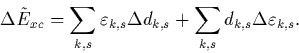
These are rearranged and substitutions made to eliminate $\Delta c_l$and $\Delta d_{l,s}$, leaving terms in only $\Delta S_{ij}, \Delta G_{kl}, \Delta H_{kl}$ and $\Delta \varepsilon_{k,s}$. $\Delta \varepsilon_{k,s}$contains terms in $\Delta \langle \tilde{n}_s \rangle_k$ and $\Delta \langle \tilde{n}^2_s \rangle_k$ which can be determined from Equations 3.2.23 and 3.2.27. Although T_ij and S_ij only depend on R_la through the basis functions, $\phi_i({\bf r} - {\bf R}_a)$, the pseudopotential term is also dependent on R_la due to $V_a^{ps}({\bf r} - {\bf R}_a)$; this is determined by integrating by parts to replace with terms in $\Delta \phi$:

The forces are relatively quick to evaluate compared to determination of the self-consistent energy.