Constraining Bond Lengths

  

Figure 6.1: Schematic of interstitial oxygen in silicon. For explanation of the labelling, see text.

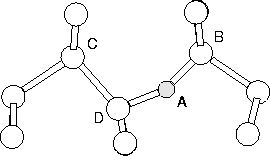
Suppose that an atom A is hopping from one site to another, during which one bond A-B is broken and the bond A-C is created (see Figure 6.1). Then a constraint is introduced on the relative bond lengths, r_A-B and r_A-C, and the cluster relaxed maintaining this constraint. The actual constraint used is

c₁ = r_A-B²-r_A-C²

Now c₁ is clearly negative in the configuration where the bond A-B is short and positive in the configuration where the bond A-C has been formed.

The saddle point usually, but not always, corresponds to a value of c₁ around zero where the A-B and A-C bond lengths are equal. For interstitial O motion, a constraint is selected so that A, B and C correspond to the O atom and the two Si atoms which swap bonds with O. However, the imposition of one constraint is insufficient [128]. During the hop, the O atom initially bonded to the Si atoms D and B, becomes bonded to D and C. However at the same time the Si atom D also breaks a bond with C and makes a bond with B. To deal with this a second constraint is required. Here,

c₂ = r_D-B²-r_D-C².

In the initial configuration c₁, c₂ are both negative but become positive after the hop. The cluster is relaxed using a conjugate gradient algorithm subject to these constraints for a range of values of c_i. The saddle point can then be directly found by interpolation on the resultant 2D energy surface.