Pure InP

  Initial investigations centred on pure InP, in order to determine vibrational frequencies and a phonon dispersion curve, and to obtain a set of Musgrave Pople interatomic potentials for frequency calculations in the defect clusters.

After relaxation, we obtained central InP bond lengths of 2.480Å along the $\langle$111$\rangle$ axis parallel to the C_3v axis, and 2.421Å otherwise (an error of 2.4% and 4.7% respectively, as the experimental bond length is 2.54 Å[49]). The bond elongation in the (111) direction is due to the intrinsic dipole moment of a bond centred cluster. The nearest neighbour P-In-P bond angle was 111.5$^\circ$, and 107.3$^\circ$ when using the In-P bond parallel to the C_3v axis; these are within 2$^\circ$ of the tetrahedral angle.

 

$$k_\theta k_{r\theta} k_{\theta \theta}$$ Atom k_r k_rr

In 7.187 0.088 -0.125 0.283 0.013

P 7.187 0.154 -0.156 0.917 0.065

We next fitted the Musgrave Pople potential to the derivatives for the inner eight atoms (this is described further and the potential given in Section 2.8.2). The coefficients are shown in Table 4.1.

 

Location Mode Neutron Raman Far I.R. Theoretical

Diffraction Scattering

(300K)[63] (300K)[64] (20K)[65]

$$\Gamma$$ LO 345.4 351 354.80

$$\pm$$ TO 303.3 354.80

$$\pm$$ X(1,0,0) LO 328.5 324.59

$$\pm$$ TO 326.5 317.46

$$\pm$$ LA 190.5 186.86

$$\pm$$ TA 67.5 69.59

$$\frac{1}{2} \frac{1}{2} \frac{1}{2} \pm$$ LO 340.5 (5,6) 335.27

$$\pm$$ TO 315.5 (4) 314.03

$$\pm$$ LA 167.5 171.19

$$\pm$$ TA 53.5 49.49

  

Figure: Calculated Phonon Dispersion Curve for InP. $\times$=Koteles et al [65], $\circ$=Hilsum et al [64], $\triangle$=Borcherds et al [63]

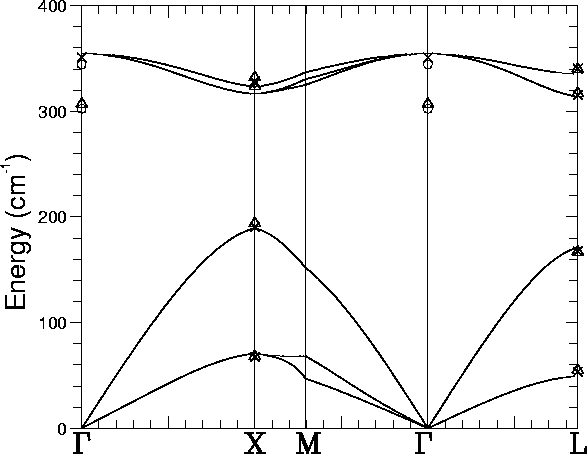A supercell calculation of the full phonon dispersion curve was performed using the Musgrave-Pople interatomic potential. This is given in Figure 4.2 along with various experimental values. Selected values from this curve are given in Table 4.2. We do not obtain any LO-TO splitting because of an absence of long range electric field effects in the potential. The highest bulk phonon modes are 354.80 (351), 324.59 (328.5), and 335.27 cm^-1 (340.5) at $\Gamma$, X, and L respectively (the experimental modes are in brackets[65], at 20K), thus our frequency errors are $\approx$ 4 cm^-1. The calculated band gap for InP was 0.84 eV, compared to an experimental value of 1.34 eV deduced from optical data[66], and is in good agreement with a previous LDF value of 0.8 eV[67] (see Section 4.2 above). Our calculated band gap is underestimated, which is unusual for a cluster calculation.

We conclude that our method gives bond lengths and local vibrational modes within an acceptable error range.