The 4 O di-y-lid thermal donor

The structure of the di-y-lid is somewhat different to that of the STDs examined in the previous chapter. The defect consists of a pair of oxygen dimers; all the other atoms are lattice Si. These dimers lie in the same $\langle$110$\rangle$ plane but are separated by two empty Si-Si bonds; the electrical activity occurs when the inner pair of O atoms become trivalent, both bonding to the central lattice Si (see Figure 9.4). The defect has no oxygen atoms on the C₂ axis along $\langle$100$\rangle$ , consistent with the EPR and ENDOR data available on the thermal donors. Crucially it has a double donor level very close to the conduction band. Since at anneal temperatures this would normally be depopulated, in all of the simulations discussed below we have modelled the defect in the +2 charge state, i.e. this shallow level is depopulated. Exceptions to this are discussed in the text.

The cluster used was Si₇₉H₆₈O₄, charged +2. Weak additional quadratic spring potentials (k_r = 5.0 eV/Ų) were used to constrain the surface H atoms, in order to simulate the effect of the rest of bulk. The structure is shown in Figure 9.4, along with bond lengths (Å) and angles (degrees). The black dots mark out the ideal Si lattice sites and show the displacements and resultant stress caused by the defect. The whole cluster, with surface hydrogen atoms removed for clarity, is shown in Figures 9.7 and 9.8. These diagrams clearly show the tensile/compressive effect the defect has on the surrounding lattice. It is highly compressive along $\langle$100$\rangle$ , and tensile along $\langle$110$\rangle$ and $\langle$110$\rangle$ , at least closer to the core. The $\langle$110$\rangle$ tensile strain is only extremely weak, and it may be that the shape of our cluster, with very little bulk Si along $\langle$110$\rangle$ from the defect, provided too great a constraint in this direction.

  

Figure 9.4: The core of the di-y-lid thermal donor. Bond lengths are in Å, bond angles are in degrees. Si atoms are white, O atoms are grey. Black dots mark the ideal Si lattice sites.

The defect essentially consists of a pair of dimers separated by what would normally be two $\langle$110$\rangle$ Si-Si bonds. However the dimers have tilted in so that the inner two O atoms are somewhat overcoordinated (whether they are truly trivalent is a debatable point, since the inner Si-O bond is extremely long for a covalent bond). Meanwhile the top two Si atoms in the defect core form a shared reconstructed bond. Thus it is possible to either view the structure as a defect core with fully coordinated Si atoms and two trivalent oxygen atoms, or alternatively with two roughly divalent oxygen atoms and an undercoordinated core Si atom, whose remaining non-bonded electron pair are being electrostatically compressed by the oxygen atoms. The reconstructed Si-Si bond is extremely long, and it is possible that this is also contributing an anti-bonding state to the defect, similar to the `A-centre' (OV^-) which has a next neighbour dilated Si-Si bond, whose antibonding equivilent can act as an electron trap to make the defect negatively charged. This reconstructed bond is also important when considering strain effects of further dimer addition (see below).

Several of the core atoms move slightly away from the ideal (110) lattice plane, and without this shift the defect is not stable. All the displacements described are along the same direction. The top two Si atoms and the two core O atoms are displaced by 0.062 Å and 0.058 Å from the (110) plane respectively (these figures are the same within the numerical limits of AIMPRO). There is some assymetry in the back Si-Si bonds of the core Si atom (2.218 and 2.230 Å). The outer two O atoms are displaced out-of-plane by 0.074 Å. The other three `core' Si atoms are displaced by less than 0.025 Å. These displacements may be sufficient to explain the `slight deviations' from C_2v symmetry observed by EPR[207].

  

Figure 9.5: The top Kohn-Sham eigenvalues for the 4O_i di-y-lid model for the thermal donor. Charge state of the defect is given beneath each column. Black boxes denote filled state, white boxes for empty states. The eigenvalues have been arbitrarily scaled to the experimental band gap of 1.16eV.

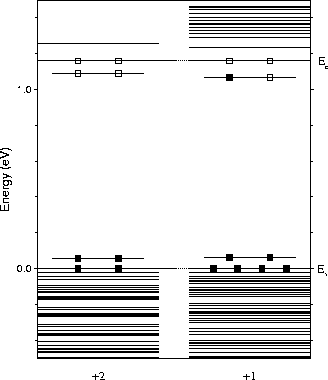The Kohn-Sham eigenvalues are given in Figure 9.5, scaled to the experimental band gap of 1.16 eV. As can be seen, the defect possesses a shallow double donor level which is depopulated in the +2 charge state. Adding a single electron to the system and relaxing once more does not produce any significant change in structure or vibrational modes. The donor level appears to drop very slightly away from the conduction band in this case. Slices through the donor wavefunction are shown in Figure 9.6. Note that in practise the donor states will be effective-mass like and will be considerably more delocalised, however they are confined here in a finite cluster.

  

Figure 9.6: Cross-sections through the Kohn-Sham wavefunction for the donor state of the di-y-lid thermal donor model in the +2 charge state. Vertical direction is $\langle$001$\rangle$ , horizontal direction is (a) $\langle$110$\rangle$ , (b) $\langle$110$\rangle$ .

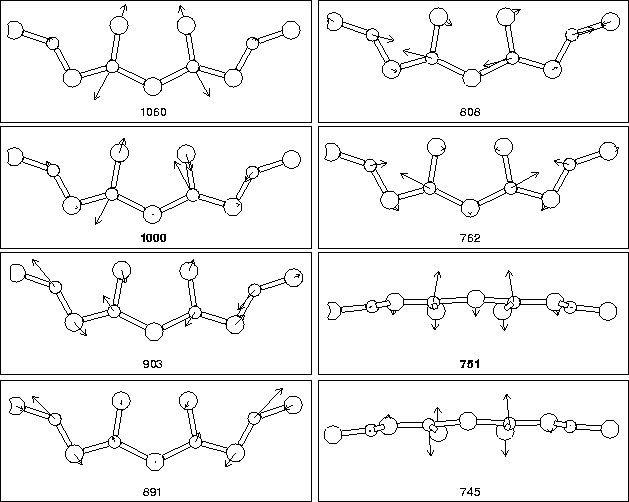
We next examined the vibrational modes of the defect core, along with the square of the dipole moment for each mode, which is linearly proportional to its absorption strength in FTIR. The results are given in Table 9.2. As can be seen, there are two modes lying at 999 cm^-1 and 734 cm^-1 which are more intense than the others. We also examined the shift in these modes with differing oxygen isotope, in Table 9.2. The agreement with the experimentally observed LVMs for the thermal donors is remarkable. Unfortunately the accuracy of our method does not allow us to distinguish between the different thermal donors, whose vibrational modes only differ by a few wavenumbers. There is however agreement with the observed TD3 LVMs to less than 0.5% in the higher mode, with $\sim$3% error in the lower mode. The core atom displacements associated with each mode are shown in Figure 9.9. It can be seen that the two most intense modes are primarily a high frequency asymmetric oxygen stretch mode associated with the core O_i atoms (stretch in the $\langle$001$\rangle$ direction), and a lower frequency out-of-plane wag mode with the two core O_i atoms once more, this time vibrating in phase. Thus they crudely approximate to a coupled stretch, and a wag mode.

 

LVM (Dipole moment)² Source ¹⁶O ¹⁷O ¹⁸O

(cm^-1) (Intensity)

1050 0.126 4lExperiment

0.249 TD2 988 945

903 0.206 724

891 0.151

808 0.190 TD3 999 955

762 0.019 728 0.323

745 0.001 Di-ylid 1000 976 955

633 0.113 751 738 726

  

Figure 9.7: Side view of the 4O_i atom di-y-lid TD. This shows the complete cluster except for the surface hydrogen atoms. The oxygen atoms are shown in black.

  

Figure 9.8: Overhead view of the 4O_i atom di-y-lid TD. This shows the complete cluster without surface H atoms. The tensile stress in the $\langle$110$\rangle$  and $\langle$110$\rangle$ is visible in the distortion to the lattice.

  

Figure 9.9: Displacement of the core atoms associated with each calculated LVM (given in cm^-1). Vector length has been exaggerated for clarity. Overhead views of the 751 and 745 cm^-1 modes have been displaced slightly off axis so that it is possible to separate the vectors due to the O and Si atoms in the core. Stronger modes are given in bold.