Approximation to the charge density

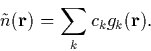
The approximate charge density is expanded in a set of basis functions [38,39],

 

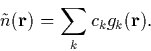$$\tilde{n}({\bf r}) = \sum_k{c_kg_k({\bf r})}.$$ (19)

We can now write an approximation to the Hartree energy in Equation 2.4.15. This is always lower than E_H, but tends to E_H as $\tilde{n}({\bf r})$ tends to $n({\bf r})$ and so provides a way of estimating the quality of the basis function fit,

 

$$\tilde{E}_H = \int \frac{n({\bf r}_1)\tilde{n}({\bf r}_2)}{\... ...bf r}_2)}{\vert{\bf r}_1 - {\bf r}_2\vert}d{\bf r}_1d{\bf r}_2.$$ (20)

Then we can select c_k in Eq. 3.2.7 to minimise the error

 

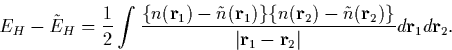$$E_H - \tilde{E}_H = \frac{1}{2}\int{\frac{\{n({\bf r}_1) - \... ...r}_2)\}}{\vert{\bf r}_1 - {\bf r}_2\vert}d{\bf r}_1d{\bf r}_2}.$$ (21)

If this is now differentiated with respect to c_k in order to determine the minimum we get an important expression,

Evaluation of these `t matrices' is often the slowest step in these cluster calculations, so obviously a careful choice of fitting function, g_k, is required. Simple Gaussian functions have the advantage of being analytically soluble, but if there are roughly as many g_k as basis functions $\phi_i$ (commonly the case), this means the t matrices are still O(N³) integrals. Nonetheless, this is the way all the O in Si work was performed. However it is possible to split the g_k into two types of function,

The first of these gives a Gaussian potential,

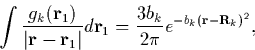$$\int{\frac{g_k({\bf r}_1)}{\vert{\bf r} - {\bf r}_1\vert}d{\bf r}_1} = \frac{3b_k}{2\pi}e^{-b_k({\bf r}-{\bf R}_k)^2},$$ (22)

making t_ijk a simple product of three Gaussians which is quick to calculate. However the form of these expressions means that their integral vanishes, and hence they do not contribute to the total charge density. Therefore the second set of expressions for g_k are introduced (simple Gaussians) to ensure the integrated charge density gives the correct number of electrons.

  This formalism was adopted for the III-V work in Chapter 4, however when testing different fitting functions for small Si-O based molecules such as disiloxane, (SiH₃)₂O, we found that a much better fit was obtained using simple Gaussian functions. Therefore these have been used for all the Si work despite the loss in computing speed.

The exchange-correlation is similarly approximated as

$$\tilde{E}_{xc} = \int \varepsilon_{xc}(\tilde{n}_\uparrow, \tilde{n}_\downarrow)\tilde{n} d{\bf r}.$$ (23)

However the expression used to minimise the error in $\tilde{n}$ for E_H (Equation 3.2.9) was integrated over all ${\bf r}$and does not necessarily minimise the error at any specific value of ${\bf r}$. Therefore it is necessary to choose a new approximation for $\tilde{n}_s({\bf r})$ and a good choice is a sum of Gaussians,

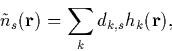$$\tilde{n}_s({\bf r}) = \sum_k d_{k,s}h_k({\bf r}),$$ (24)

with d_k,s obtained by minimising

$$\int \left\{ n_s({\bf r}) - \tilde{n}_s({\bf r})\right\}^2 d{\bf r}.$$ (25)

If this is differentiated with respect to d_k,s we obtain

The integrals are the same for both s, and if g_k is set to the first form in Equation 3.2.13 then u_ijk are just proportional to t_ijk which makes calculation extremely quick.